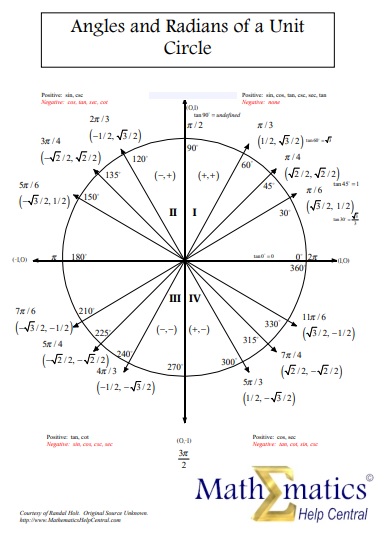
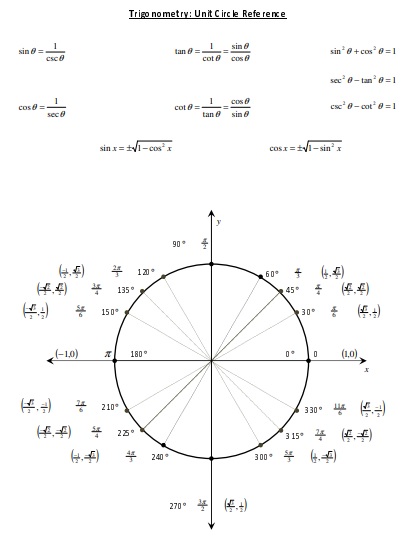
A unit circle chart is a platform used to demonstrate trigonometry. This diagram is used to describe all possible measures of angles from 0-degrees to 360-degrees. All the negatives and positive angles in the circle are explained by it. For measuring angles, a circle gives a much broader range. Therefore, instead of a right triangle people use this shape.
You measure the positive angles in a unit circle by using the initial side of the positive x-axis. You, then move towards the terminal side. In a counterclockwise direction, do so around the point of origin. The chart would show positive angles represented in radians and degrees. The angles’ terminal sides form lines that are straight. 30 and 210-degrees, 60 and 240-degrees, and so on are some examples of these angle measurements.
Unit or radian circle charts also indicate negative angles aside from positive angles. It’s a fact that various basic angles have negative values and multiples of themselves. You need to measure the angles in a clockwise direction in order to get these values. For example, a 30-degree angle is the similar as a -330-degree angle because their terminal sides are the same.
There are several ways you can name angles. You can get endless angle measures when you perform a complete rotation of the circle. During the rotation, you can do this when you add or subtract 360-degrees. Before settling on the terminal side of the angle, do these. After that, you can obtain the positive and negative values of the similar basic angle.
Table of Contents
How to draft a unit circle chart?
Drafting a unit circle diagram is quite simple if you have all the steps to do so. You have to take all the right triangles and the angles of the unit circle and then put them together. This way, you will create the complete unit circle. When you do this, you have to make special triangles one at a time.
Moreover, the trig function values would remain the same no matter how long the sides you use are for the angle in a triangle. Mathematicians made all the sides of the triangle smaller in order to make things easier. Below are some tips that you can follow to make your own unit or radian circle chart;
- At first, on a graph, start in the first quadrant and make a 30-degree angle for your unit circle.
- Carefully, draw the angle and with the use of a straight line, link it to the origin.
- You should also ensure that in the first quadrant, there is the terminal side of your 30-degree angle. Furthermore, ensure that the angle’s size is fairly small. Between 0 and 90-degrees, it should only be a third of the way.
- Then, draw a perpendicular line. When you do this, you will be able to make a right triangle.
- The triangle’s hypotenuse would act as the radius of your unit circle. One of the legs would be on the x-axis and the other would be on the y-axis.
- Next, you have to find the length of the hypotenuse. Bear in mind that the radius is always 1 with a unit circle. This shows that the hypotenuse of the triangle would also be 1.
- Also, you have to find the length of the other sides of the triangle. Start with the shorter side in order to do this. By dividing the value by 2, find the length. You have to multiply the value of the short side by 2 for the long side.
- Next, you need to determine the point on your circle. There is a unit circle on a coordinated plane that has the origin at its center. Thus, every point on the circle has distinct coordinates. By now, on your unit circle, you should be able to assign a name to the point at the 30-degree angle.
- It would be a lot easier to find the points of the other angles on your circle when you’ve done all these steps.
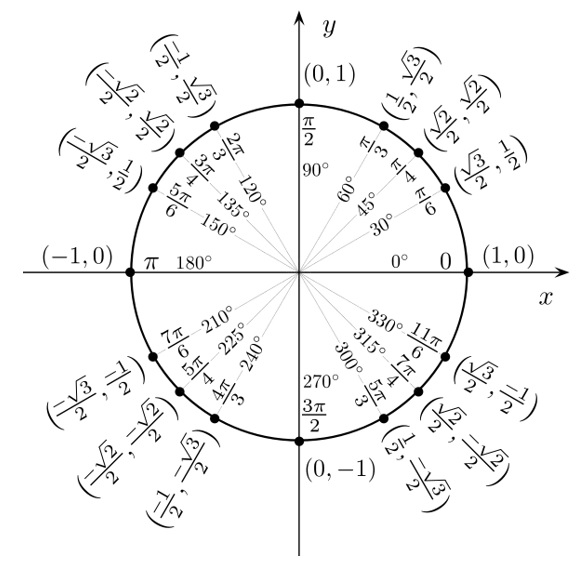
- The 2nd and 4th quadrants just have mirror images of quadrant 1. However, the signs differ. The reason behind is that the points on the circle are in varying locations of the plane.
Here are some facts that you have to know regarding a trig circle/trigonometry circle chart;
- There are positive x and y values in the first quadrant.
- The second quadrant has a negative x value and a positive y value.
- There are negative x and y values in the third quadrant.
- The fourth quadrant has a positive x value and a negative y value.
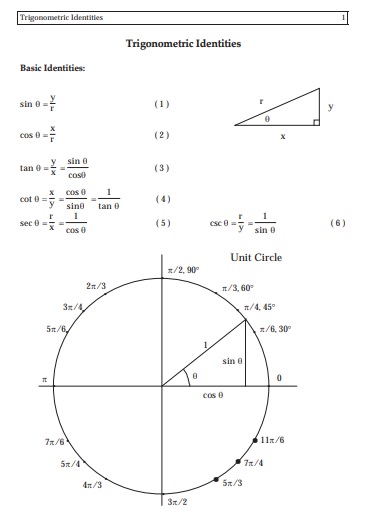
These are all parts of the whole entire unit circle. Sin, cos, tan, sec, csc, cot are also involved in the unit circle chart. You may also like Venn Diagram Templates.
Printable Unit Circle Chart
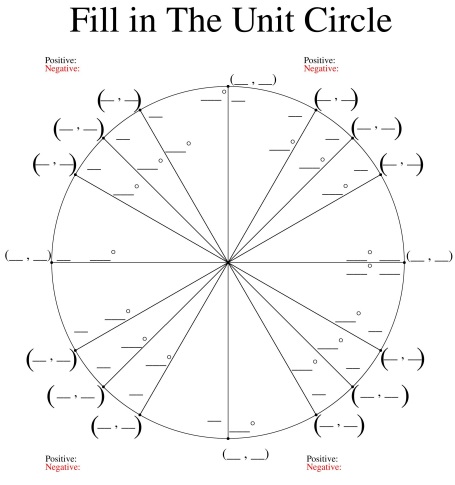
Fill in The Unit Circle PDF
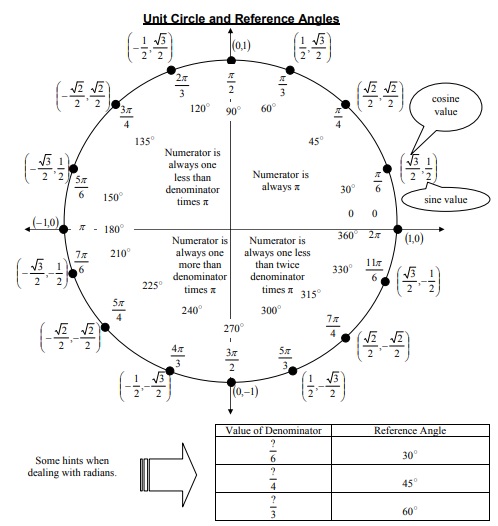
Unit Circle and Reference Angles
Trig Cheat Sheet
Free Unit Circle Chart
Blank Unit Circle Chart
Trigonometric Identities Cheat Sheet
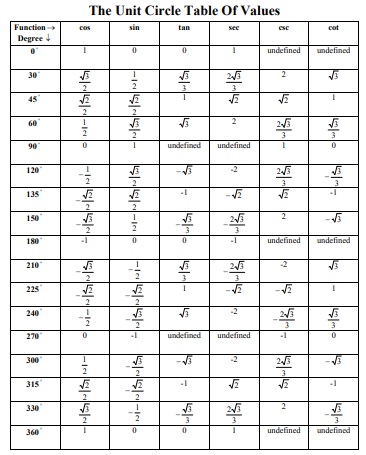
The Unit Circle Table of Values
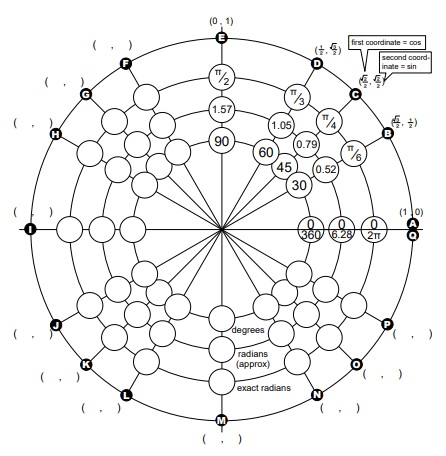
The Unit Circle Exact Measurements and Symmetry
The Unit Circle Explorers Guide
Unit Circle Worksheet
Angles and Radians of a Unit Circle
Trigonometry Unit Circle Reference
Trigonometric Formula Sheet
Let us understand a unit circle:
You can use a unit circle diagram when you are dealing with trigonometry. The unit circle chart is one of the best tools that you can use. You can download a unit circle printable and work with it instead of making your own unit circle. Below are some tips that will help you out;
What a unit circle is
You should first know what it is before understand it. A unit circle is actually a circle having a radius of 1 that’s centered at the origin. This circle can be used to find special trigonometric functions and ratios. Around the unit circle, a number line is wrapped. When you’re evaluating trig functions, this acts as the input value.
The 6 basic trig ratios
Sin cos tan sec csc cot ratios are included in a unit circle. You need to know the following ot understand the chart;
- sinθ = opposite/hypotenuse
- cosθ = adjacent/hypotenuse
- tanθ = opposite/adjacent
- cscθ = 1/sinθ
- secθ = 1/cosθ
- cotθ = 1/tanθ
What a radian is
A radian is considered as an alternative way to measure angles. A one radian is an angle you require. Thus, the length of the radius would be equal to the enclosed arc length. The circle’s size or orientation isn’t significant. However, you must know how many radians are there in the entire circle. A full circle has 2π radians to make things easier for you.
Be able to convert between degrees and radians competently
You need to be able to convert values competently in case you want to understand a radian circle chart. We have mentioned above that a full circle has 2π radians. Let us discuss below some quick conversions for you;
- 2πradian = 360degree and vice versa.
- Radian = (360/2π) degree and vice versa.
- Radian = (180/π) degree and vice versa.
The “special” angles
There are some special angles such as π/6, π/3, π/4, π/2, π, and all their multiples that you have to know and remember.
Keep in mind the trig identities that give the 6 basic trig functions for angles
There are trig identities that give the 6 basic trig functions for angles. You should know them if you want to understand unit circles, charts, and diagrams. Let us discuss below the identities of a unit circle chart;
- sinθ = y
- cosθ = x
- tanθ = y/x
- csc = 1/y
- sec = 1/x
- cot = x/y
Locate and keep in mind the 6 basic trig functions for the angles on the axes
Locating the trig functions of angles which are the multiples of π/2 is quiet easy. These involve 0, π/2, π, 3π/2, 2π, and so on. All you have to do is imagine the angle on the axes. Sin will either be 1 or -1 in case the angle’s terminal side is along the y-axis. While, sin will be 0 if the angle’s terminal side is along the x-axis and its cos will either be 1 or -1.
Locate and keep in mind the 6 basic trig functions of π/6, which is a special angle
To do this, on your unit circle, start by drawing the π/6 angle. Keep in mind that special triangles have varying side lengths. These are 45-45-90 and 30-60-90 and short side of the triangle is half of the hypotenuse. So,
- sinπ/6 = 1/2
- cosπ/6 = (√3)/2
- tanπ/6 = 1/(√3)
- cscπ/6 = 2
- secπ/6 = 2/(√3)
- cotπ/6 = √3
Locate and keep in mind the 6 basic trig functions of π/3, which is a special angle
This angle is less complex as compared to the previous one. It contains a point on the circle’s circumference. In the π/6 angle, the x-coordinate equals the y-coordinate at that point. Hence,
- sinπ/3 = (√3)/2
- cosπ/3 = 1/2
- tanπ/3 = √3
- cscπ/3 = 2/(√3)
- secπ/3 = 2
- cotπ/3 = 1/(√3)
Locate and keep in mind the 6 basic trig functions of π/4, which is a special angle
You’ll use the ratios for a 45-45-90 triangle for this one. So, the basic trig functions if plotted on a unit circle are;
- sinπ/4 = 1/(√2)
- cosπ/4 = 1/(√2)
- tanπ/4 = 1
- cscπ/4 = √2
- secπ/4 = √2
- cotπ/4 = 1
Determine reference angle to make use of
Now, you have already understood the trig values of the special angles. π/6, π/3, and π/4 are these special reference angles. But, all these angles lie in the first quadrant. You need to know which reference angle to use if you need to locate a function of a smaller or larger special angle. Furthermore, the reference angle you need generally relates to the same family of angles. You have to reduce the fraction as much as you can to identify.